Depth of Cut

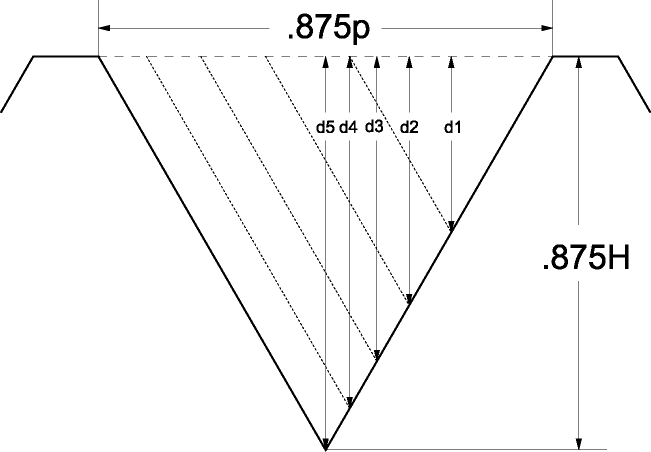
For reference, here are same basic formulas for calculating The Area of Some Simple Polygons.

Basically, the area removed on each pass is equal. The area of a triangle is base times width divided by 2. So the total area = (0.875p x 0.875H) / 2 = (0.875p x 0.875 x 0.866p) / 2 = 0.3315 x p x p (or 0.3315 x p squared)

Using the formula from the previous step (which preserves the angle) we get total area = (0.875p x 0.875 x p/( 2 * tan( 30 ))) / 2 = 49 x p x p / ( 64 * 4 * tan( 30 )) = (49 x p x p) / (256 * tan(30)). I converted the 0.875 back into 7/8 to give integer numbers.

For a given depth d, d = base / (2 x tan(30)), so base = 2 x d x tan( 30 ), and the area = (base x depth) / 2 = (2 x d x tan(30)) x d / 2 = d x d x tan(30), so we can calculate d = sqrt( area / tan(30))

In this example, we're doing 5 passes, each with an equal area. So d1 = sqrt( 1/5 of total area / tan(30)). d2 = sqrt( 2/5 of total area / tan(30)), and so on.

The thread22 program allows a Ratio value to be specified to allow the last pass to be some percentage of the other passes. If we wanted 5 passes with Ratio set to 0.4, then the formula for the area of pass 1 would be 1/4.4, and the area for the 2nd pass would 2/4.4 an so on. Generalizing for pass i would give (i / ((num_passes - 1) + ratio) x total_area) except for the last pass which would use the total_area. Bigger...